News & Events
Exploring the World of Geometry: Shapes, Angles, and More

Geometry word is derived from the ancient Greek word “geometron”, in which geo means “earth” and Metron means “measurements”. Geometry has been carried on from one ancient civilization to another for thousands of years, such as Egypt, Greece, Babylonia, India and China. Ancient people used geometry for constructing buildings such as the Great Pyramid of Giza in Egypt and temples such as the Kailasa temple in Maharashtra. They used the principles of geometry to enhance their constructions. However, the Greeks made it more systematic by introducing the concept of proofs. Proof is a method by which a statement/ assumption is determined as false or true with the help of logic and facts.
Contributions in geometry
A notable work in the field of geometry is Euclid's Elements, given by the Greek mathematician Euclid. Euclid elements contain postulates, propositions, theorems and construction. With the help of postulates and axioms, Euclid geometry studied solid shapes and figures. Another advancement in geometry occurred with the introduction of coordinate geometry, which uses coordinates and equations. Two novel branches of geometry, called hyperbolic and elliptical geometry, came into existence after some mathematicians disagreed with the fifth postulate given by Euclid. However, the geometry that we use today is primarily based on Euclid geometry.
Major concepts of geometry
Though geometry contains a wide range of topics and concepts, here are some that will give you a basic understanding of geometry. This includes points, lines, space and many more, which are considered the fundamental block of geometry, so let us get started.
1. Point
A point is a dot on a piece of paper, so it can’t be defined with length, height, and width. Almost everything in space starts from a point, whether a line, circle, rectangle or polygon.
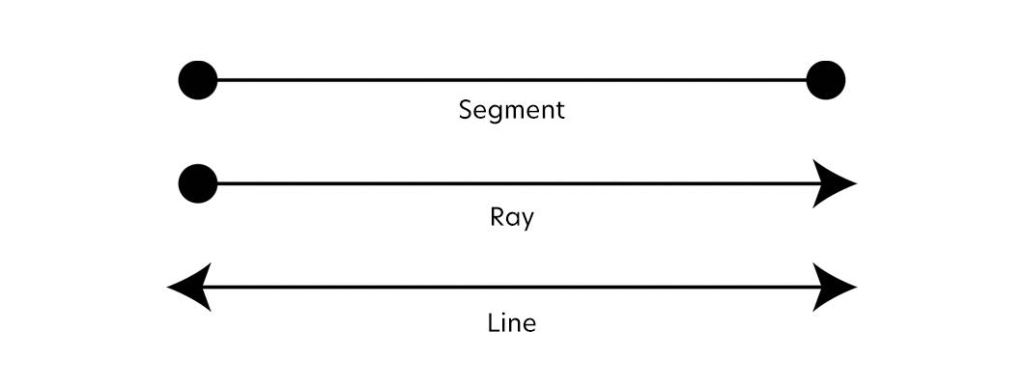
2. Line, line segment and ray
A line is formed by connecting a set of points in a straight path and extending infinitely in both directions. It has length but not height and width. On the other hand, a line segment has a starting and an endpoint. A ray, on the other hand, is a line that has a starting point but no endpoint.
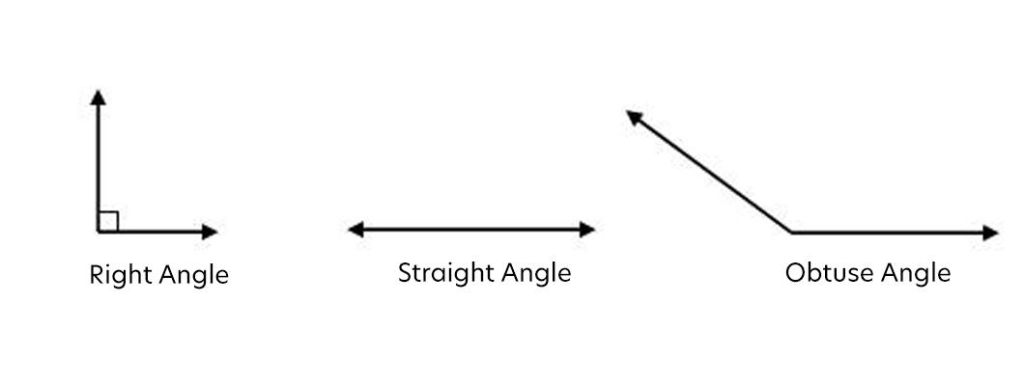
3. Angles
Angles are formed when two rays meet at a common point (endpoint) also called the vertex of the angle. Some common types of angles are right, obtuse, and straight angles.
- Right angle- The right angle makes an angle of 90 degrees. It is represented by a square symbol or by “90”.
- Obtuse angle- Obtuse angle is an angle of more than 90 but less than 180 degrees. It is wider than the right angle- but not like a straight line.
- Straight angle- Straight angle is an angle of 180 degrees or the angle made by a straight line.
In below fogure, you can see the different type of Angles:
4. Polygon
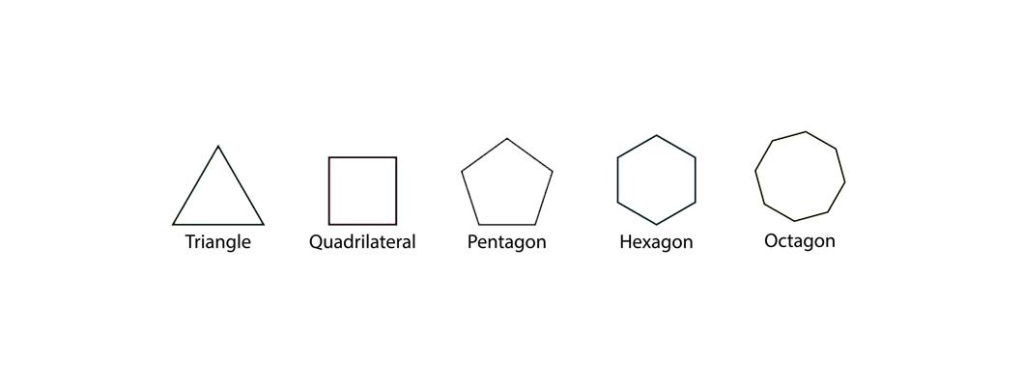
A polygon is a two-dimensional shape that has a finite number of sides. It is formed by connecting straight-line segments and should have a minimum of three sides. Some common types of polygons are triangles, quadrilaterals, pentagons, hexagons, octagons and many more. These are 2-dimensional shapes which had two parameters- length and width.
| Polygon | Number of sides |
| Triangle | 3 |
| Quadrilateral | 4 |
| Pentagon | 5 |
| Hexagon | 6 |
| Octagon | 8 |
In below figure, you can see the different types of Polygons:
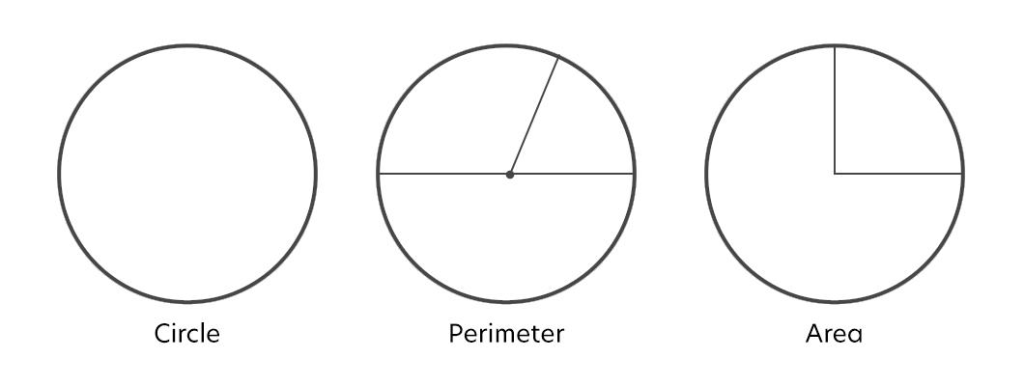
5. Circle, perimeter, and area
A circle is the simplest shape in geometry. The distance from the centre to any point of the circle is called the radius, and twice the radius is called the diameter. Geometrical formulas associated with a circle are as follows.
Circumference:- C=2πr
where r is the radius of the circle and π=3.14
Area= πr²
where r is the radius of the circle
But what are area and perimeter? Let us find out their meaning.
The space occupied by a shape is determined by area, whereas the perimeter measures the outline/length of a shape.
For example, the area of square= side^2
The perimeter of the square= 4*side
(Because the square has four sides, and we have to consider the length of the shape).
In below figure, you can see the Circle, Perimeter and Area:
6. Three-Dimensional shapes (3-D shapes)
The three parameters of a 3-D shape are length, width, and height. These are defined by their properties, such as edges, faces, vertices, curved surfaces, volume, etc. Some common 3-D shapes in geometry are cubes, cuboids, cones, cylinders and spheres. The following table will help you understand the 3-D shapes in geometry.
| 3-D shape | Properties |
| Cube | 6 square faces, 8 vertices and 12 edges |
| Cuboid | 6 rectangular faces, 8 vertices and 12 edges |
| Cone | 2 faces, 1 vertex and 1 edge |
| Sphere | 1 curved surface, 0 edges and vertices |
| Cylinder | 3 faces, 2 edges and 0 vertices |
In below figure, you can see the different types of 3-D Shapes
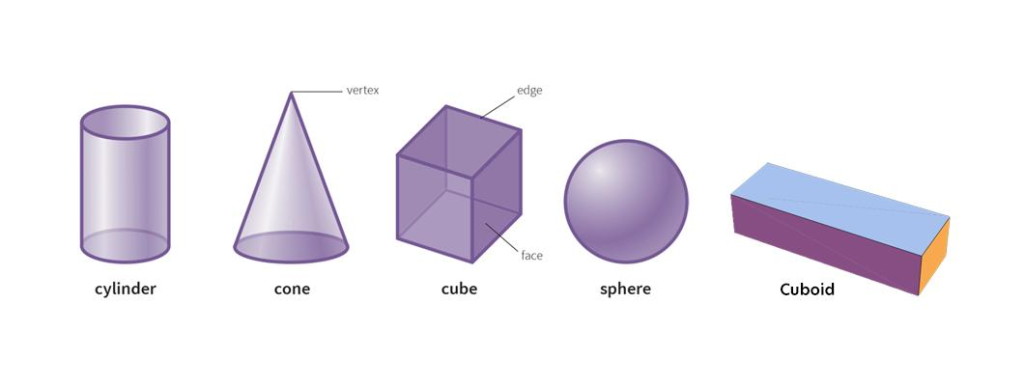
Faces, edges and vertices
As mentioned above, faces, edges and vertices are the three most essential parameters of a 3-D dimensional shape. Let us explore what are these below:
Faces- In 3-D shapes, a flat or curved surface is called a face.
Edges- It is a line segment that connects two faces.
Vertices- A point at which two edges meet is a vertex.
Geometry in the Indian education system
An international public school or other schools affiliated with state boards and CBSE educate children (around grades 6 to 8) on geometry concepts such as polygon, congruence, etc. As the children move to higher grades (9 to 10), children are introduced to 3-D shapes. There are also many questions asked from geometry in competitive examinations, such as JEE (Joint Entrance Examination) and CAT (Common Admission Test). Also, a good understanding of geometry helps students excel in exams and develop problem-solving skills, logical reasoning, and spatial awareness.
The key takeaways
At last, we have curated this article to help you understand the fundamentals of geometry and unlock the doors of future education. Keep reading our writings to read topics that cover a wide range of fields/subjects.

